English Version

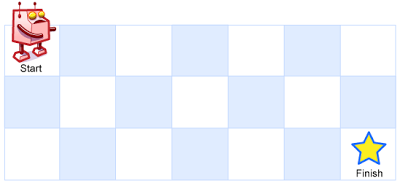
设想有个机器人坐在一个网格的左上角，网格 r 行 c 列。机器人只能向下或向右移动，但不能走到一些被禁止的网格（有障碍物）。设计一种算法，寻找机器人从左上角移动到右下角的路径。

网格中的障碍物和空位置分别用 1 和 0 来表示。

返回一条可行的路径，路径由经过的网格的行号和列号组成。左上角为 0 行 0 列。

示例 1:

输入: [   [0,0,0],   [0,1,0],   [0,0,0] ] 输出: [[0,0],[0,1],[0,2],[1,2],[2,2]] 解释: 输入中标粗的位置即为输出表示的路径，即 0行0列（左上角） -> 0行1列 -> 0行2列 -> 1行2列 -> 2行2列（右下角）

说明：r 和 c 的值均不超过 100。

我们可以使用深度优先搜索来解决本题。我们从左上角开始，向右或向下移动，直到到达右下角。如果在某一步，我们发现当前位置是障碍物，或者当前位置已经在路径中，那么我们就返回，否则我们将当前位置加入路径中，并且标记当前位置为已经访问过，然后继续向右或向下移动。

如果最终能够到达右下角，那么我们就找到了一条可行的路径，否则说明不存在可行的路径。

时间复杂度 $O(m \times n)$，空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别是网格的行数和列数。

classSolution: defpathWithObstacles(self, obstacleGrid: List[List[int]]) ->List[List[int]]: defdfs(i, j): ifi>=morj>=norobstacleGrid[i][j] ==1: returnFalseans.append([i, j]) obstacleGrid[i][j] =1if (i==m-1andj==n-1) ordfs(i+1, j) ordfs(i, j+1): returnTrueans.pop() returnFalsem, n=len(obstacleGrid), len(obstacleGrid[0]) ans= [] returnansifdfs(0, 0) else []

classSolution { privateList<List<Integer>> ans = newArrayList<>(); privateint[][] g; privateintm; privateintn; publicList<List<Integer>> pathWithObstacles(int[][] obstacleGrid) { g = obstacleGrid; m = g.length; n = g[0].length; returndfs(0, 0) ? ans : Collections.emptyList(); } privatebooleandfs(inti, intj) { if (i >= m || j >= n || g[i][j] == 1) { returnfalse; } ans.add(List.of(i, j)); g[i][j] = 1; if ((i == m - 1 && j == n - 1) || dfs(i + 1, j) || dfs(i, j + 1)) { returntrue; } ans.remove(ans.size() - 1); returnfalse; } }

classSolution { public: vector<vector<int>> pathWithObstacles(vector<vector<int>>& obstacleGrid) { int m = obstacleGrid.size(); int n = obstacleGrid[0].size(); vector<vector<int>> ans; auto dfs = [&](thisauto&& dfs, int i, int j) -> bool { if (i >= m || j >= n || obstacleGrid[i][j] == 1) { returnfalse; } ans.push_back({i, j}); obstacleGrid[i][j] = 1; if ((i == m - 1 && j == n - 1) || dfs(i + 1, j) || dfs(i, j + 1)) { returntrue; } ans.pop_back(); returnfalse; }; returndfs(0, 0) ? ans : vector<vector<int>>(); } };

funcpathWithObstacles(obstacleGrid [][]int) [][]int { m, n:=len(obstacleGrid), len(obstacleGrid[0]) ans:= [][]int{} vardfsfunc(i, jint) booldfs=func(i, jint) bool { ifi>=m||j>=n||obstacleGrid[i][j] ==1 { returnfalse } ans=append(ans, []int{i, j}) obstacleGrid[i][j] =1if (i==m-1&&j==n-1) ||dfs(i+1, j) ||dfs(i, j+1) { returntrue } ans=ans[:len(ans)-1] returnfalse } ifdfs(0, 0) { returnans } return [][]int{} }

functionpathWithObstacles(obstacleGrid: number[][]): number[][]{constm=obstacleGrid.length;constn=obstacleGrid[0].length;constres=[];constdfs=(i: number,j: number): boolean=>{if(i===m||j===n||obstacleGrid[i][j]===1){returnfalse;}res.push([i,j]);obstacleGrid[i][j]=1;if((i+1===m&&j+1===n)||dfs(i+1,j)||dfs(i,j+1)){returntrue;}res.pop();returnfalse;};if(dfs(0,0)){returnres;}return[];}

implSolution{fndfs(grid:&mutVec<Vec<i32>>,path:&mutVec<Vec<i32>>,i:usize,j:usize) -> bool{if i == grid.len() || j == grid[0].len() || grid[i][j] == 1{returnfalse;} path.push(vec![i asi32, j asi32]); grid[i asusize][j asusize] = 1;if(i + 1 == grid.len() && j + 1 == grid[0].len()) || Self::dfs(grid, path, i + 1, j) || Self::dfs(grid, path, i, j + 1){returntrue;} path.pop();false}pubfnpath_with_obstacles(mutobstacle_grid:Vec<Vec<i32>>) -> Vec<Vec<i32>>{letmut res = vec![];ifSelf::dfs(&mut obstacle_grid,&mut res,0,0){return res;}vec![]}}

classSolution{privatevarans=[[Int]]()privatevarg:[[Int]]=[]privatevarm:Int=0privatevarn:Int=0func pathWithObstacles(_ obstacleGrid:[[Int]])->[[Int]]{ g = obstacleGrid m = g.count n =g[0].count returndfs(0,0)? ans :[]}privatefunc dfs(_ i:Int, _ j:Int)->Bool{if i >= m || j >= n || g[i][j]==1{returnfalse} ans.append([i, j])g[i][j]=1if(i == m -1 && j == n -1) || dfs(i +1, j) || dfs(i, j +1){returntrue} ans.removeLast()returnfalse}}